- 1. Introduction
- 2. The Limits of Determinism
- 3. Backtracking Implementation
- 4. Backtracking to Binary Palindromes
- 5. BNF Parsing, Revisited
- 6. Extended BNF
- 7. EBNF in EBNF
- 8. Parsing EBNF Grammars
- 9. A Recursive Descent Parser Generator
- 10. Our Very Own Programming Language
- 11. Semantic Analysis, Revisited
- 12. A New Programming Language in < 100 Lines
- 13. Wrapping Up
You’ve been tasked to implement a parser for yet another language—one with the brevity of COBOL and the readability of APL. You’re sick of writing parsers. Surely a computer can do it, right?
This post was derived from a Jupyter notebook.
1 Introduction
So there you are, sitting for a job interview, when you’re asked to solve the famous FizzBuzz problem. You can use any language you like, and you’re given as much time as you need. If only there were a programming language you liked. Then you think, “Surely, they’ll hire me if I design and implement a programming language, and then use that to solve FizzBuzz! I’d be a shoo-in, right?” Maybe, maybe not. (And don’t call me “Shirley.”) Regardless, it’s a long road to dazzling/baffling your interviewer in this way.
At the outset of the previous post, we couldn’t even recognize strings of balanced parentheses properly; by the end, we had developed an array of parsing techniques, introduced syntax-directed translation, and implemented a very basic calculator program. Along the way, we dealt with a number of problems that arise in implementing parsers.
One of those problems had its origin in writing a parser for BNF grammars, specifically that the absence of a rule end delimiter led to confusion in how to interpret the identifiers introducing new rules. For example, the toy grammar
a : b c d d : e f g
could not be properly analyzed by a parser that only considered one token of lookahead at a time (or, at least, at all times). Our way through it last time was to strategically outfit the parser with lookahead predicates—additional parsers that, while consuming no input, nevertheless enforced conditions on the input stream. For handwritten parsers for a wide range of practical languages, it’s a good strategy, since the parsing behavior is easy to reason about. There is, however, another option that is both generally applicable and that doesn’t require modifying the grammar.
There’s much to discuss. In brief, we will:
- Highlight the limits of deterministic parsing methods and introduce the technique of backtracking;
- Reimplement our parsing utilities to use a backtracking strategy by default;
- Use those utilities to construct a parser for BNF grammars;
- Extend the syntax of BNF to more easily describe languages we actually care about;
- Automatically generate parsers from EBNF grammars; and,
- Use a generated parser to implement a programming language.
We’ll end with an implementation of FizzBuzz in our very own programming language, implemented in turn with our very own parser generator.
2 The Limits of Determinism
Consider the following toy grammar:
bin_palin :
| ZERO
| ONE
| ZERO bin_palin ZERO
| ONE bin_palin ONE
This describes all bit strings that also happen to be palindromic (i.e., the same forward and backward). Implementing this using the parsing utilities from before,
@parser def ONE(s): return literal('1', s) @parser def ZERO(s): return literal('0', s) @parser def bin_palin(s): ''' bin_palin : | ZERO | ONE | ZERO bin_palin ZERO | ONE bin_palin ONE ''' return alt(seq(ONE, bin_palin, ONE), seq(ZERO, bin_palin, ZERO), ONE, ZERO, EPSILON)(s)
Now let’s try a few cases. First, an empty string:
bin_palin('')
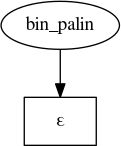
Now, a zero:
bin_palin('0')
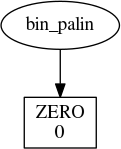
So far, so good. Now, let’s try a pair of zeros:
bin_palin('00')
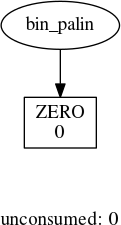
Here, it seems to have confused itself for some reason. To find that reason, let’s look at the transition function for a PDA that can recognize this language:
| state | stack | input | stack operations | next state | consume input? |
|---|---|---|---|---|---|
| scan | ’0’ | ’0’ | pop | scan | yes |
| scan | ’1’ | ’1’ | pop | scan | yes |
| scan | bin_palin |
any | pop | scan | no |
| scan | bin_palin |
any | poppush ’0’, bin_palin, ’0’ |
scan | no |
| scan | bin_palin |
any | poppush ’1’, bin_palin, ’1’ |
scan | no |
| scan | ’$’ | ’$’ | pop | accept | yes |
The expansion of bin_palin is not uniquely determined—i.e., our PDA is a
non-deterministic PDA (NPDA). What’s more, every parsing mechanism we’ve
implemented so far operates deterministically. This is the very problem that led
us to considering an additional symbol of input for the BNF parser: If we were
to write a transition table for that language, we’d find that it’s
non-deterministic if we only considered one token of input at a time. By looking
ahead one more token, we in a sense created a new PDA whose transition function
used pairs of tokens instead of single tokens (though, for brevity, it ignored
that second input token most of the time).
Unlike the BNF parsing problem, however, there is no amount of lookahead that will help us here, as palindromic strings do not have any sort of marker to help us identify the middle of the input stream. While we could write a parser that uses a huge amount of lookahead that allows us to deal with any string we might likely encounter, we know perfectly well that longer strings are theoretically possible, and it’s only a matter of time before technology or an attacker throws one at us and breaks our parser. What we need is a way to simulate non-determinism. The simplest is to allow the parser to consume the same input at different times, i.e., to backtrack arbitrarily far in the input stream and try something else.
Before moving on, it should be clear that NPDAs can recognize languages that deterministic PDAs (DPDAs) cannot—specifically, DPDAs can recognize a class of languages called deterministic context-free languages, while NPDAs can recognize all context-free languages.
3 Backtracking Implementation
While there are more pieces to implementing backtracking than for lookahead
predicates, it’s still quite straightforward. The key is to get alt to return
all possible parses from the current input position. Since there might be quite
a lot of them, we’ll put generators to good use:
def alt(*ps): def parse(s): return (item for p in ps for item in p(s)) return parse
Now, since an alt-parser will produce a series of possible parses, it follows
that a seq-parser that calls one will, too:
def seq(*ps): def parse(s): if ps: for first, rest in ps[0](s): if ps[1:]: for cont, rest2 in seq(*ps[1:])(rest): yield [first] + cont, rest2 else: yield [first], rest return parse
Since alt and seq now expect generators, we’ll make our terminal parsers
into generators as well:
def literal(spec, s): spec = spec.strip() n = len(spec) s = s.lstrip() if s[:n] == spec: yield spec, s[n:] def match(spec, s): s = s.lstrip() m = re.match('(%s)' % spec, s) if m: g = m.group(0) yield g, s[len(g):]
And we’ll finish up by modifying the wrapper class for parser functions:
class parser: def __init__(self, f): self.f = f def __call__(self, s): for matched, rest in self.f(s): sym = symbol(self.f.__name__, matched) yield parse_result((sym, rest)) @parser def EPSILON(s): yield '', s
In general, we’re only interested in parses that consume the entire input stream:
def parses(start, s): for x in start(s): p, rest = x if not rest.strip(): yield p
Very often, we’re happy with the first such parse:
def parse(start, s): return next(parses(start, s))
4 Backtracking to Binary Palindromes
We’re now ready to attack the palindrome problem. The parsing functions look just as they did before:
@parser def ZERO(s): return literal('0', s) @parser def ONE(s): return literal('1', s) @parser def bin_palin(s): ''' bin_palin : | ZERO | ONE | ZERO bin_palin ZERO | ONE bin_palin ONE ''' return alt(seq(ZERO, bin_palin, ZERO), seq(ONE, bin_palin, ONE), ZERO, ONE, EPSILON)(s)
But we use them a bit differently, since each parser now generates a series of parses. For the case ’00’,
parses(bin_palin, '00')
there is precisely one parse, which looks like
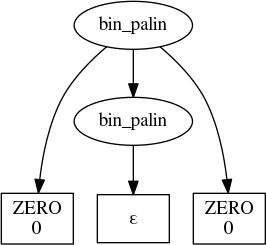
5 BNF Parsing, Revisited
With our new-found power, let’s try parsing BNF again. The code is the same as our first attempt (the one without additional lookahead):
## terminals @parser def IDENTIFIER(s): return match('[a-zA-Z_][a-zA-Z_0-9]*', s) @parser def COLON(s): return literal(':', s) @parser def PIPE(s): return literal('|', s) ## nonterminals @parser def production(s): ''' production : | IDENTIFIER production ''' return alt(seq(IDENTIFIER, production), EPSILON)(s) @parser def productions(s): ''' production : production PIPE productions | production ''' return alt(production, seq(production, PIPE, productions))(s) @parser def rule(s): 'rule : IDENTIFIER COLON productions' return seq(IDENTIFIER, COLON, productions)(s) @parser def rules(s): ''' rules : | rule rules ''' return alt(seq(rule, rules), EPSILON)(s)
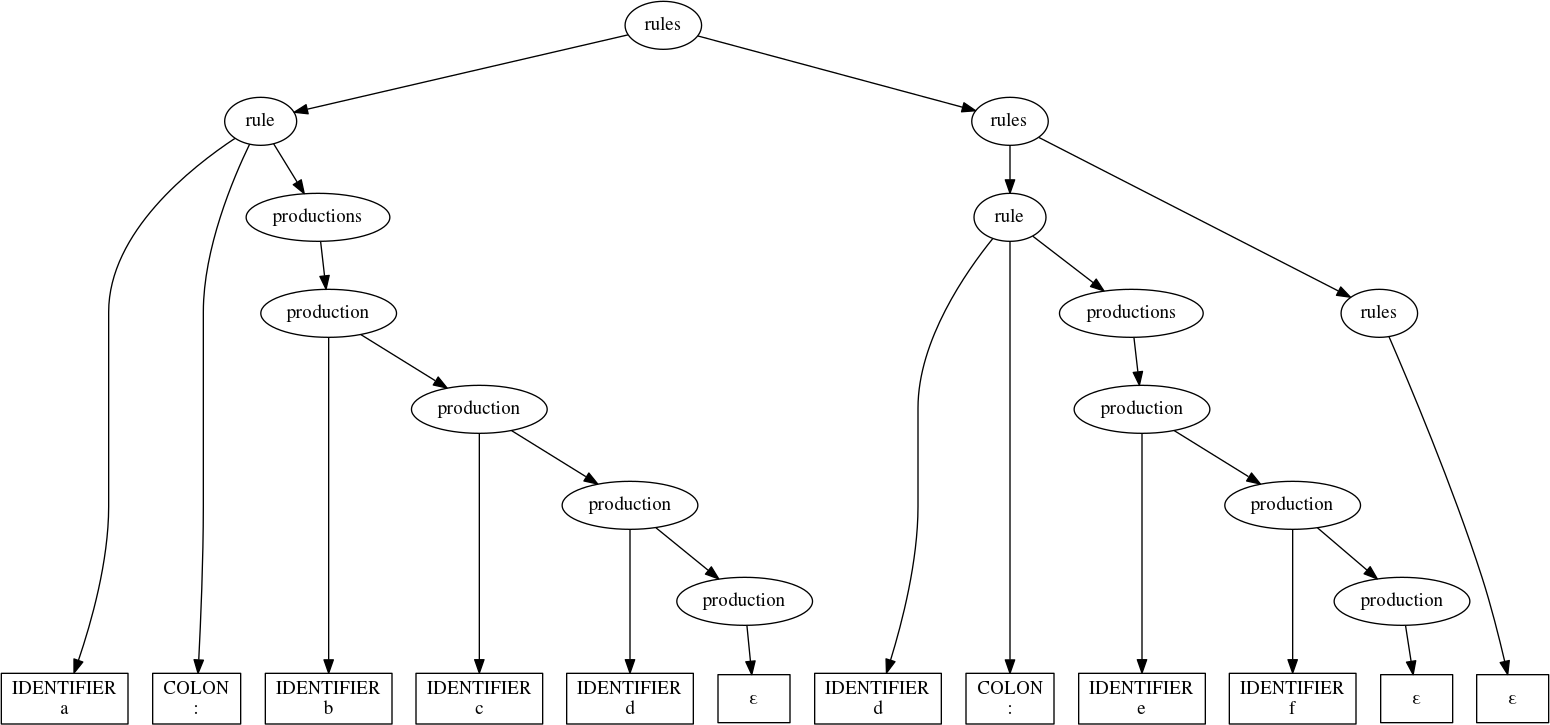
Applying this to the toy grammar first caused us to stumble now gives the proper result:
parse(rules,
'''
a : b c d
d : e f
''')
6 Extended BNF
All of the grammars we’ve looked at so far have used productions like
list_of_something :
| something list_of_something
and
list_of_something : something list_of_something
| something
to express repetition. For example, the BNF grammar for BNF grammars from the previous post described series of rules as
rules : rule rules
| rule
and series of productions as
productions : production PIPE productions
| production
while productions themselves were described by
production :
| IDENTIFIER production
Likewise, we’ve used productions like
optional_item :
| item
to describe substitutions that may or may not happen. For example, the toy grammar for nested parentheses, braces, etc. was
parens :
| LPAREN parens RPAREN parens
Whenever we program, we mercilessly root out needless repetition, even of form, and the same is true of writing grammars. What we need is a notation that allows us to concisely express repetition and optional constructs in a grammar. Luckily, we’re not the first to desire an Extended Backus-Nauer Form (EBNF). There are many flavors of EBNF adding different sets of notational conveniences, but we’ll stick with just repetition and options.
First, we’ll denote any number of repetitions of a set of productions by enclosure in braces; so,
foo : {bar}
says that a foo is a sequence of any number of bars. Using this
notational convenience, we can describe vanilla BNF (i.e., unextended) with the
much more compact grammar
rules : rule {rule}
rule : IDENTIFIER COLON productions
productions : production {PIPE production}
production : {IDENTIFIER}
Secondly, we’ll denote optional units by enclosing them in bracketes, allowing us to write
parens : [LPAREN parens RPAREN parens]
Now that we understand what we want from these syntactic extensions, let’s write
the code that implements them, starting with repetition. Because of
backtracking, a repeated parser might match multiple substrings from the same
position; this is the same behavior that shaped the backtracking implementation
of seq. Unlike seq, where we know how many symbols (determined by the
grammar) are to be parsed from the input, we have no idea how many repetitions
we’ll see—it’s entirely data dependent, and depending on the data source it
might be quite large. Rather than risk a RuntimeError due to excessive
recursion, we’ll use an iterative implementation with an explicit stack to
manage the search for a valid parse.
def rep(p): def parse(s): stack = [([], s)] while stack: path, s = stack.pop(-1) yield path, s for x, rest in p(s): if len(rest) < len(s): # EPSILON can cause infinite loopiness stack.append((path + [x], rest)) return parse
The utility to create optional parsers is much more boring:
def opt(p): return alt(p, EPSILON)
7 EBNF in EBNF
Describing BNF with EBNF is nice, but if we’re going to try writing grammars in EBNF, it might be worth considering how that notation should really look—i.e., let’s try to come up with a grammar for EBNF. We’ll start with a series of rules, defined as before:
rules : {rule}
rule : IDENTIFIER COLON productions
Productions are unchanged:
productions : production {PIPE production}
It’s in productions that we want to start bending the syntax. Rather than
saying
production : {IDENTIFIER}
we’ll have the more general idea of a substitution:
production : {substitution}
What kind of substitutions? Well, we know we want to be able to reference other rules (like before). We also want to be able to use the repeated and optional syntaxes that we just discussed; and, since we’re enclosing things in brackets and braces, let’s allow parentheses for simple grouping:
substitution : repeated
| optional
| enclosed
| IDENTIFIER
repeated : LBRACE productions RBRACE
optional : LBRACK productions RBRACK
enclosed : LPAREN productions RPAREN
For the final increment of convenience, let’s allow direct usage of string literals and regular expressions. With that,
substitution : repeated
| optional
| enclosed
| IDENTIFIER
| STRING_LITERAL
| REGEX
There’s one more development, and it’s purely to simplify things later: identifiers play a dual role in EBNF, allowing us to name rules and to reference other rules. To capture that, we’ll factor substitution just a bit:
substitution : repeated
| optional
| enclosed
| reference
| STRING_LITERAL
| REGEX
reference : IDENTIFIER
8 Parsing EBNF Grammars
You’ll notice that, despite allowing for in-line regexes and string literals in a grammar, our EBNF grammar still doesn’t use such conveniences. That’s intentional, as we don’t yet have the machinery for dealing with them, and we’re trying to maintain a close correspondence between our grammars and our code. We’ll get to use the full power of our EBNF soon enough.
First, let’s define some utilities to help us:
### Something not discussed above is that it might be nice to have comments in ### a grammar. Rather than clutter the EBNF grammar directly, we'll just build ### comment handling into the first part of parsing terminals. def skip_comment(s): s2 = re.sub('^#[^\n]*', '', s.lstrip()).lstrip() while s2 != s: s = s2 s2 = re.sub('^#[^\n]*', '', s.lstrip()).lstrip() return s def literal2(spec, s): return literal(spec, skip_comment(s)) def match2(spec, s): return match(spec, skip_comment(s))
The terminal parsers that we really want to define:
@parser def IDENTIFIER(s): return match2(r'[a-zA-Z_][a-zA-Z0-9_]*', s) @parser def STRING_LITERAL(s): return match2(r"\'(\\.|[^\\'])*\'", s) @parser def REGEX(s): return match2(r'/(\\.|[^\\/])+/', s)
And the terminal parsers that we’re defining because we still have to:
@parser def LBRACE(s): return literal2('{', s) @parser def RBRACE(s): return literal2('}', s) @parser def LBRACK(s): return literal2('[', s) @parser def RBRACK(s): return literal2(']', s) @parser def LPAREN(s): return literal2('(', s) @parser def RPAREN(s): return literal2(')', s) @parser def COLON(s): return literal2(':', s) @parser def PIPE(s): return literal2('|', s)
Now we can focus on the main grammar:
@parser def rules(s): 'rules : {rule}' return rep(rule)(s) @parser def rule(s): 'rule : IDENTIFIER COLON productions' return seq(IDENTIFIER, COLON, productions)(s) @parser def productions(s): 'productions : production {PIPE production}' return seq(production, rep(seq(PIPE, production)))(s) @parser def production(s): 'production : {substitution}' return rep(substitution)(s) @parser def substitution(s): ''' substitution : repeated | optional | enclosed | reference | STRING_LITERAL | REGEX' ''' return alt(repeated, optional, enclosed, reference, STRING_LITERAL, REGEX)(s) @parser def enclosed(s): 'enclosed : LPAREN productions RPAREN' return seq(LPAREN, productions, RPAREN)(s) @parser def repeated(s): 'repeated : LBRACE productions RBRACE' return seq(LBRACE, productions, RBRACE)(s) @parser def optional(s): 'optional : LBRACK productions RBRACK' return seq(LBRACK, productions, RBRACK)(s) @parser def reference(s): 'reference : IDENTIFIER' return IDENTIFIER(s)
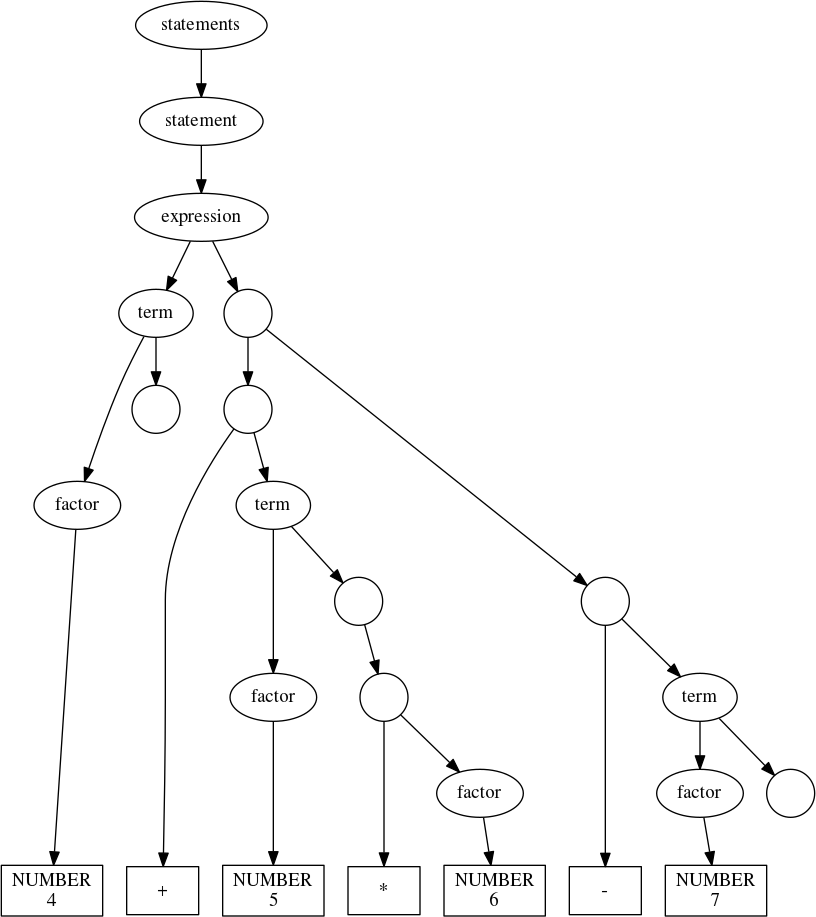
With that, we can rewrite the grammar for the “calculator” language from before like so:
CALCULATOR = ''' statements : {statement} statement : assignment | expression assignment : IDENTIFIER '=' expression expression : term {/[+-]/ term} term : factor {/[*\/]/ factor} factor : reference | NUMBER | enclosed reference : IDENTIFIER enclosed : '(' expression ')' IDENTIFIER : /[A-Za-z_]\w+/ NUMBER : /[0-9]+/ '''
When parsed with rules, we get the following structure:

The empty circles you see are the anonymous nonterminals produced by rep and
opt—remember, they’re containers for sets of productions. You’ll notice that
some have no child nodes; those each correspond to zero repetitions of the
relevant nonterminal. For example, the first rule in the calculator grammar,
statements : {statement}
has only one production, so the list of alternative productions, described in the grammar for EBNF as
{PIPE production}
is empty. The leftmost and topmost of the nameless, childless circles in the tree above corresponds to that empty list.
This is also a good time to point out that the body of that repetition is
actually an anonymous seq,
PIPE production
which is why the immediate descendents of the nodes representing lists of alternate productions are themselves anonymous nonterminals.
9 A Recursive Descent Parser Generator
Consider how we’ve been writing parsers so far: We define a grammar, perhaps something like
uberpwn : pleasantries order condition COMMA recipient PERIOD pleasantries : YOU MAY order : FIRE condition : WHEN YOU ARE READY recipient : GRIDLEY
and then we write parsing functions by inspection that are little more than the rules with some boilerplate:
@parser def uberpwn(s): 'uberpwn : pleasantries order condition COMMA recipient PERIOD' return seq(pleasantries, order, condition, COMMA, recipient, PERIOD)(s)
We could avoid a great deal of typing, and potential for bugs, if we could somehow generate the parsing functions from the grammar. A program that allows us to do that is called a parser generator. Leaning on the existing parsing functions for EBNF, as well as a custom postorder evaluator for the parse tree of an input grammar, a workable solution might look like:
## utilities to clean things up def dummy_parser(parsefn): parsefn.__name__ = '' return parser(parsefn) def Literal(spec): return dummy_parser(lambda s: literal2(spec, s)) def Match(spec) : return dummy_parser(lambda s: match2(spec, s)) def enclosure(sym): return type(sym) == list def nonterminal(sym): return not (isinstance(sym, symbol) and sym.terminal) def combine(parts, fn): if len(parts) == 0: return EPSILON elif len(parts) == 1: return parts[0] else : return fn(*parts) def parserize(parsefn): return parsefn if isinstance(parsefn, parser) else parser(parsefn) ## the parser generator class Parser: def __init__(self, start, grammar, **symbols): self.start = start self.grammar = grammar self.symbols = symbols self._eval(next(parses(rules, grammar))) def handle(self, sym): handler = getattr(self, 'h_' + sym.type, None) if handler: hargs = [sym.value] if sym.terminal else sym.value sym.result = handler(*hargs) return sym.result def subeval(self, sym): for child in sym: self._eval(child) def _eval(self, sym): self.subeval(sym) if not enclosure(sym): self.handle(sym) def __call__(self, s): return parse(self.symbols[self.start], s) #### handlers def h_enclosed(self, _, body, __): return body.result def h_optional(self, _, body, __): return opt(body.result) def h_repeated(self, _, body, __): return rep(body.result) def h_substitution(self, subst) : return subst.result def h_STRING_LITERAL(self, s): return Literal(s[1:-1]) def h_REGEX (self, r): return Match (r[1:-1]) def h_reference(self, name): return lambda s: self.symbols[name.value](s) def h_production(self, *substs_): substs = [subst.result for subst in substs_ if subst] return combine(substs, seq) def h_productions(self, first, rest): prods = [first.result] + [prod.result for (_, prod) in rest] return combine(prods, alt) def h_rule(self, name_, _, prods): parsefn = parserize(prods.result) parsefn.f.__name__ = name = name_.value self.symbols[name] = parsefn
Of particular interest is how evaluation is controlled. Before, we used a purely syntax-directed strategy to control statement evaluation in our interactive calculator. The parser for that language, though, was deterministic, so we knew that there would never be more than one parsing from a given position in the input stream. The parser for EBNF employs backtracking to simulate nondeterminism. If we were to invoke a handler for a symbol immediately on recognition, all of the work performed by that handler would be wasted were we to backtrack later. What’s more, any of that handler’s side effects would persist, possibly leading to strange interactions between parsing attempts.
Rather than use that excellent recipe for bugs, we instead adopted the approach
of finding a valid parse tree for the entire input first, and only then trying
to evaluate it. Thus, Parser.eval is written to traverse a finished parse
tree, invoking handlers for the various symbols as it encounters them. (To be
clear, Parser.eval is meant only to apply to the parse trees of EBNF grammars;
we’ll write something more general shortly.)
Applying Parser to the calculator grammar
calc_parser = Parser('statements', CALCULATOR)
gives us a ready tool for analyzing expressions and assignments, just as before:
calc_parser('4 + 5*6 - 7')
10 Our Very Own Programming Language
Now that we can automatically generate parsers for interesting languages, let’s create a more interesting language—let’s turn our “calculator” language into a programming language. For this demonstration, all we’ll do is bolt on syntax for loops, conditionals, and output:
statements : {statement}
statement : print # new syntax
| loop # new syntax
| conditional # new syntax
| assignment
| expression
assignment : IDENTIFIER '=' expression
expression : term {/[+-]/ term}
term : factor {/[%*\/]/ factor}
factor : reference
| NUMBER
| enclosed
reference : IDENTIFIER
enclosed : '(' expression ')'
print : 'print' (expression | STRING_LITERAL)
loop : 'while' expression statements 'end'
conditional : 'if' expression statements 'end'
NUMBER : /[-]?[0-9]+/
STRING_LITERAL : /\'(\\.|[^\\'])*\'/
# it's critical that IDENTIFIER not pick up any reserved words
IDENTIFIER : /(?!print|while|if|end)[a-zA-Z_][a-zA-Z_0-9]*/
After building a parser from this grammar,
Parser('statements', ''' statements : {statement} ... ''')
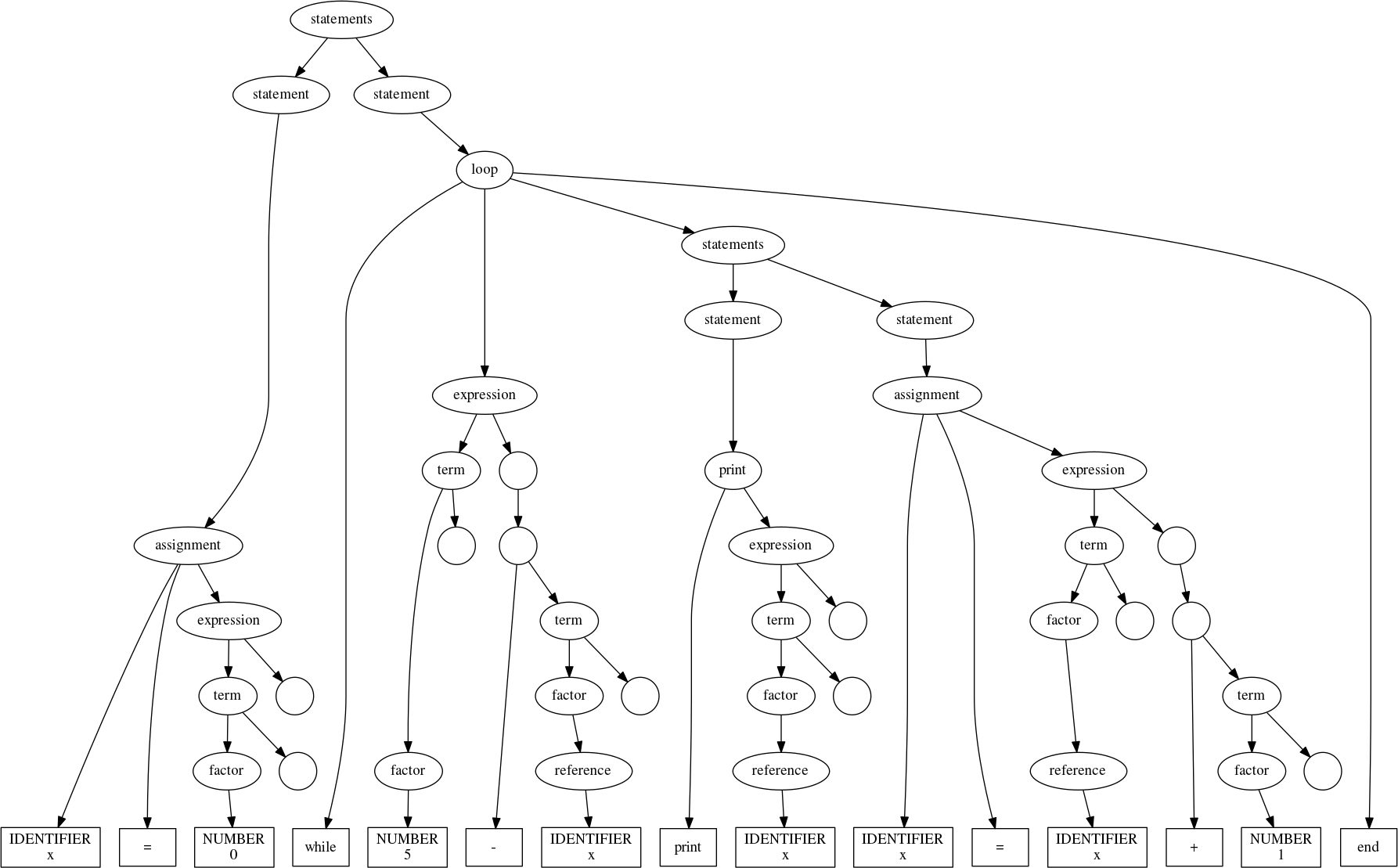
we can parse programs written in the language it describes. For example, a program to count from 0 to 4 might look like:
x = 0
while 5 - x
print x
x = x + 1
end
Parsing that program with our grammar gives
11 Semantic Analysis, Revisited
Let’s ponder how to bring our new language, and programs written in it, to life. Let’s write an interpreter.
While a strictly postorder traversal can get us pretty far, this time it’s not enough. The nature of conditional and loop statements requires us to control the evaluation of some portions of the parse tree based on the results of evaluating other portions. For example, consider the loop
while 5 - x
print x
x = x + 1
end
The loop itself consists of four major parts: an introductory keyword, a condition, a body, and an ending keyword. This is expressed in the grammar above as
loop : 'while' expression statements 'end'
To deliver the conventional semantics of a while loop, the interpreter has to repeatedly evaluate the body
print x x = x + 1
as long as x is not equal to 5. The standard behavior of a postorder
evaluator, however, is to evaluate each node of the parse tree once in a
bottom-up, left-to-right order. To gain control of when certain parse subtrees
are evaluated, we’ll introduce an additional bit of state into the
evaluator. First, we’ll split off the introductory keyword, thereby giving us a
named symbol to which we can attach a handler:
loop : WHILE expression statements 'end' WHILE : 'while'
Then we’ll create two handlers,
- One for
WHILE, which will inform the evaluator to skip normal evaluation of the condition, body, and ending keyword; and - One for
loop, which will directly control the evaluation of the condition and the body, giving us ample opportunity to implement the semantics we desire.
The evaluator class below provides the basic mechanism that we need.
class evaluator: def __init__(self): self.skip = 0 self.handler = {} # If nonzero, self.skip inhibits evaluation of the next self.skip sibling # nodes in the parse tree by left-to-right postorder evaluation. It is # reset to 0 on moving up the parse tree. This was done to allow setting # skip to, say, -1 to inhibit the remaining siblings (however many there # are) while allowing handlers higher in the tree to operate normally. def __call__(self, sym): 'evaluate the subtree rooted at sym' if self.skip: self.skip -= 1 else: return self._eval_basic(sym) def _eval_basic(self, sym): ret = None dummy = type(sym) == list if not getattr(sym, 'terminal', False): for child in sym: ret = self(child) self.skip = 0 if dummy: return ret try: handler = self.handler[sym.type] except KeyError: return except AttributeError: return hargs = [sym.value] if sym.terminal else sym.value sym.result = handler(*hargs) return sym.result def on(self, sym): 'set a symbol handler' def deco(fn): self.handler[sym] = fn return fn return deco
12 A New Programming Language in < 100 Lines
We’re now ready to implement an interpreter for our language, which we’ll give the highly informative name of ASDF. Using the grammar, parser generator, and evaluator, it comes together with very little effort:
import operator as ops class asdf_interpreter: ''' statements : {statement} statement : print | loop | conditional | assignment | expression assignment : IDENTIFIER '=' expression expression : term {/[+-]/ term} term : factor {/[%*\/]/ factor} factor : reference | NUMBER | enclosed reference : IDENTIFIER enclosed : '(' expression ')' print : 'print' (expression | STRING_LITERAL) loop : WHILE expression statements 'end' conditional : IF expression statements 'end' NUMBER : /[-]?[0-9]+/ STRING_LITERAL : /\'(\\.|[^\\'])*\'/ # it's critical that IDENTIFIER not pick up any reserved words IDENTIFIER : /(?!print|while|if|end)[a-zA-Z_][a-zA-Z_0-9]*/ # we'll put a handler on these introductions so we have the opportunity # to operate the 'skip' mechanism and control evaluation of the bodies WHILE : 'while' IF : 'if' ''' def __init__(self): self.calc = calc = evaluator() self.parse = Parser('statements', self.__class__.__doc__) self.vars = {} @calc.on('reference') def h_reference(name): return self.vars[name.value] @calc.on('NUMBER') def h_NUMBER(p): return int(p) @calc.on('enclosed') def h_enclose(_, inside, __): return inside.result @calc.on('factor') def h_factor(p): return p.result @calc.on('term') @calc.on('expression') def h_apply_ops(first, rest): OP = {'+': ops.add, '-': ops.sub, '*': ops.mul, '/': ops.truediv, '%': ops.mod} acc = first.result for (op, mag) in rest: acc = OP[op.value](acc, mag.result) return acc @calc.on('STRING_LITERAL') def h_STRING_LITERAL(s): return s[1:-1] @calc.on('assignment') def h_assignment(name, _, val): self.vars[name.value] = val.result @calc.on('print') def h_print(_, out): print(out.result) @calc.on('WHILE') @calc.on('IF') def h_compound_intro(_): calc.skip = -1 @calc.on('conditional') def h_conditional(_, cond, conseq, __): if calc(cond): calc(conseq) @calc.on('loop') def h_loop(_, test, body, end): while calc(test): calc(body) def __call__(self, prog): self.calc(self.parse(prog))
That’s it. Now all we have to do is instantiate the interpreter,
ASDF = asdf_interpreter()
write a program to solve the FizzBuzz problem,
fizzbuzz = ''' i = 1 # for demonstration, stop at 20 iterations while 21 - i fizz = 1 buzz = 1 emit = 1 if i % 3 fizz = 0 end if i % 5 buzz = 0 end if fizz * buzz fizz = 0 buzz = 0 emit = 0 print 'FizzBuzz' end if fizz emit = 0 print 'Fizz' end if buzz buzz = 0 emit = 0 print 'Buzz' end if emit print i emit = 0 end i = i + 1 end '''
and run it:
ASDF(fizzbuzz)
1 2 Fizz 4 Buzz Fizz 7 8 Fizz Buzz 11 Fizz 13 14 FizzBuzz 16 17 Fizz 19 Buzz
13 Wrapping Up
It’s virtually assured that no other candidate for a given job would dream of answering the FizzBuzz question by creating a programming language with which to solve it, and the odds that any of your competition would attempt a parser generator along the way are infinitesimal. Does this mean you’d get the job for pulling such a stunt? Not necessarily—the interviewer could just as easily call security.
But this was never about just the next gig. In this and the previous two posts we’ve examined in considerable detail, both theoretical and practical, the foundations of regular expression engines and much of what happens in compilers and interpreters. In so doing, we’ve expanded our understanding of the software that we use and build with, and we’ve gained an array of design tools—and options—that we didn’t have before.
There’s a lot we didn’t cover, too. We didn’t talk about code generation or optimization. We didn’t discuss the design of virtual machines. We didn’t even discuss alternative parsing approaches (like LL or LR or LALR). That’s okay. This post has once again run long, and we might visit at least some of those topics soon enough.